Classification: Handling class imbalance (Adult income dataset)

Analyzing and Predicting Income using Machine Learning Techniques and handling class imbalance

R
tidymodels
Author

Zahier Nasrudin

Published

August 18, 2023

Objective(s)

  1. To predict whether an individual’s annual income exceeds 50k or less (classification).
  2. To handle class imbalance.

Data Understanding

Description

Based on the website:

Extraction was done by Barry Becker from the 1994 Census database. A set of reasonably clean records was extracted using the following conditions: ((AAGE>16) && (AGI>100) && (AFNLWGT>1)&& (HRSWK>0))

Load library

Code 
library(tidyverse)
library(tidymodels)
library(scales)
library(themis)
library(knitr)
library(glue)
library(reactable)
library(reactablefmtr)

Load dataset

For this target income prediction, we will be utilizing a data-set from the UCI Machine Learning Repository called adult dataset. The link to the data-set is: https://archive.ics.uci.edu/dataset/2/adult

Code 
income_dataset <- read_csv("input/adult.csv")

To achieve our objectives of this project, the target feature is identified. It is based on the nature of the response variable (whether an individual is earning: <=50k or >50k annually)

In this dataset, you will find 48,842 rows and 15 columns:

Target feature in dataset
Target Feature Type Description
income Character <=50k or >50k
Dataset description
Feature Type Description
age Integer Individual’s age
workclass Character Individual’s sector of employment
fnlwgt Integer Final weight
education Character Highest education degree
educational-num Integer Highest education degree (Numeric form)
marital-status Character Individual’s marital status
occupation Character Individual’s occupation
relationship Character Relationship role in a family
race Character Individual’s race
gender Character Individual’s gender
capital-gain Integer Capital gain in the previous year
capital-loss Integer Capital loss in the previous year
hours-per-week Integer Working hour (per week)
native-country Character Individual’s native country

Let’s do some quick exploration, by examining the income distribution, grouped as either <=50k or >50k.

Income distribution

The plot shows the distribution of income, $50k or below or above $50k.

Code 
income_dataset %>%
  count(income) %>%
  mutate(percentage = round((n / sum(n)) * 100, 2)) %>% 
  ggplot(aes(x = fct_reorder(income, n), y = n)) +
  geom_col(width = 0.5) +
  coord_flip() +
  scale_y_continuous(labels = comma, expand = c(0,0), limits=c(0,50000)) +
  geom_text(mapping=aes(label= glue("{comma(n)} ({percentage}%)"), 
                        x = income),
            size= 3.5, hjust = -0.5, family = "Karla") +
  labs(x = "Class",
       y = "Total",
       title = "Distribution of Income")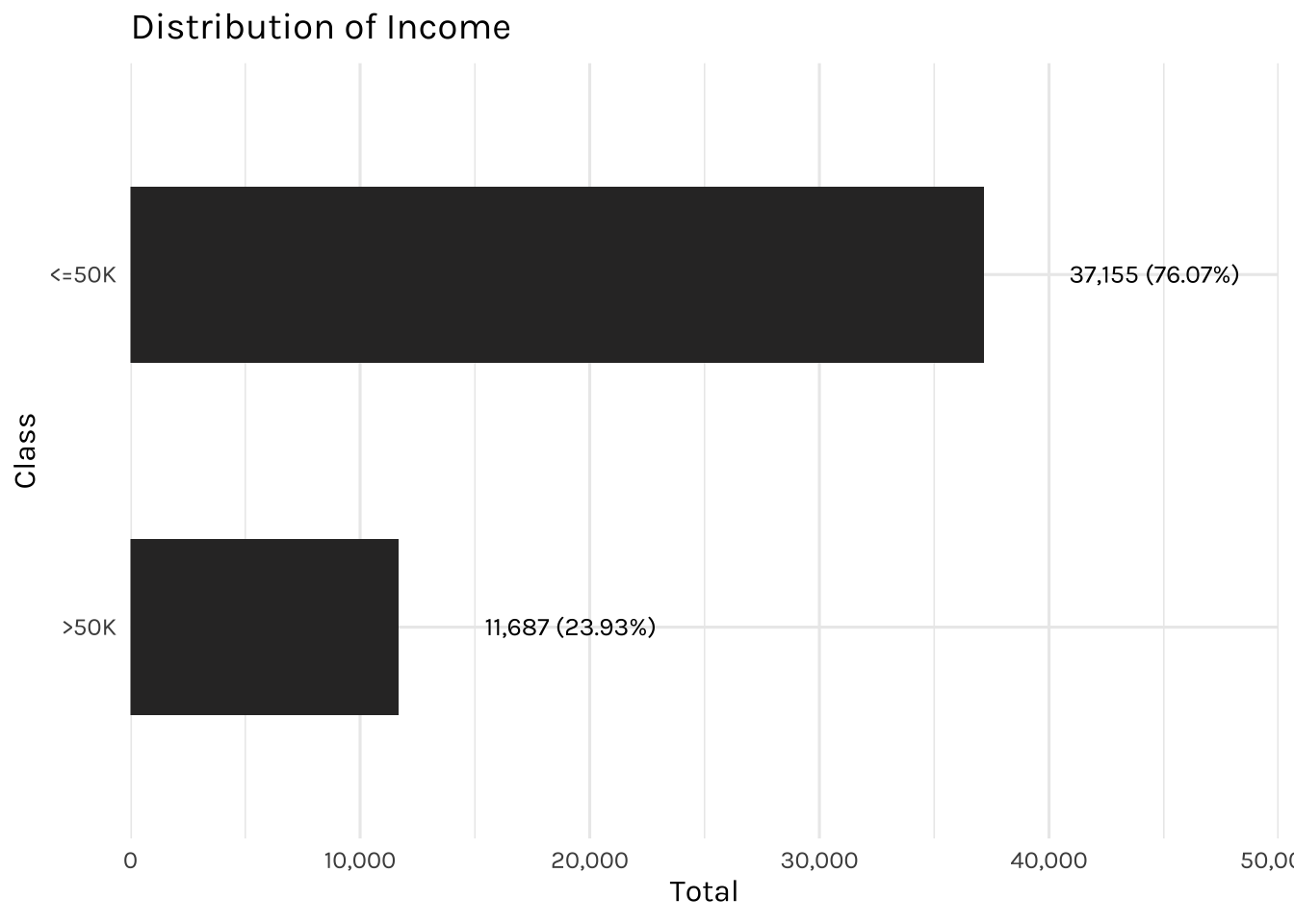

This dataset is slightly imbalanced, with the majority of individuals earning <=50k annually and the minority of individuals earning >50k.

Age

Code 
income_dataset %>%
  ggplot(aes(x = age)) +
  geom_histogram(bins = 20) +
  scale_y_continuous(expand = c(0,0)) +
  scale_x_continuous(breaks = c(seq(from = 17, to = 95, by = 10))) +
  labs(x = "Age",
       y = "",
       title = "Distribution of Age")

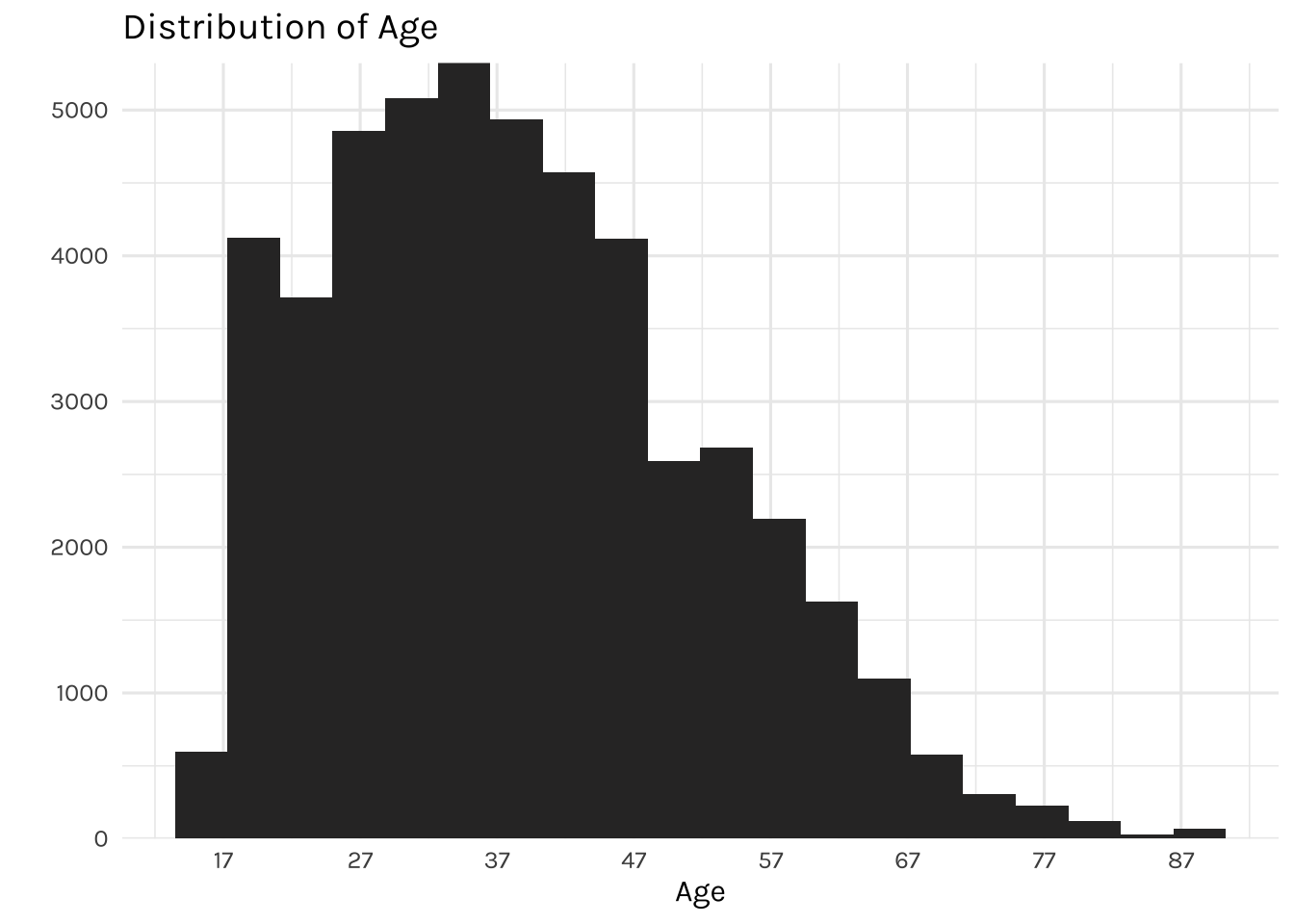
The graph above is showing the distribution of individuals by age. It displays a right-skewed distribution, where most of the individuals are falling between the ages of 27 and 47, while the youngest individual in the dataset is 17 and the oldest is 90 years of age.

Work class

Code 
## Level

desired_level_work_class <- income_dataset %>% 
  count(workclass, income) %>% 
  group_by(workclass) %>% 
  mutate(percentage = round((n / sum(n)) * 100, 2)) %>% 
  filter(income == "<=50K") %>% 
  arrange(percentage) %>% 
  pull(workclass) %>% 
  unique()


income_dataset %>%
  count(workclass, income) %>% 
  mutate(workclass = factor(workclass, levels = desired_level_work_class),
         income = factor(income, levels = c(">50K", "<=50K"))) %>% 
  ggplot(aes(x = workclass, y = n, fill = income)) +
  geom_bar(width = 0.5, position="fill", stat="identity") +
  coord_flip() +
  scale_y_continuous(labels = percent) +
  labs(title = "Percentage of income by working class",
       x = "",
       y = "",
       fill = "Income")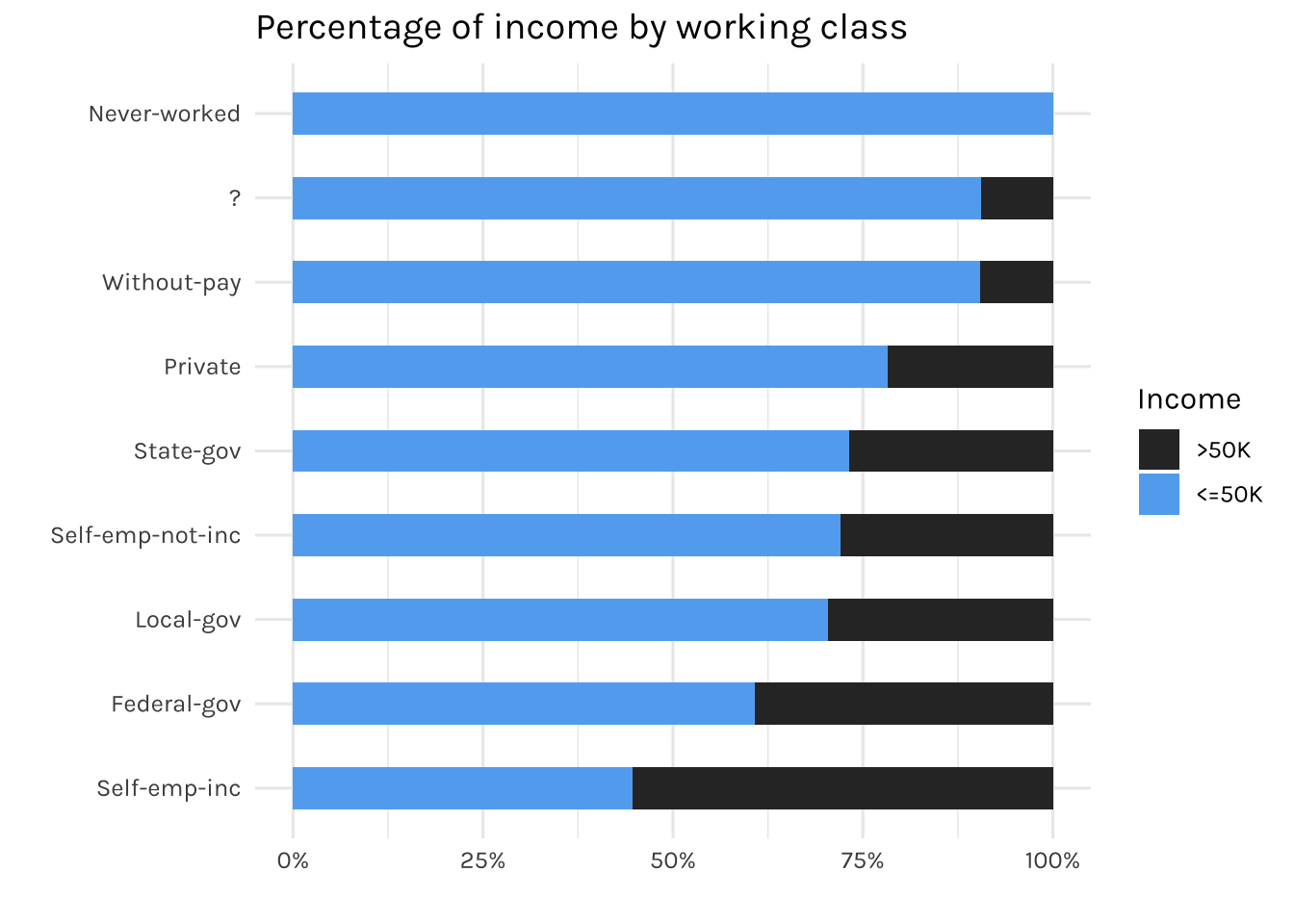

The graph displays the percentage of working-class individuals who earn <=50k or >50k annually. As expected, individuals who never worked before earned less than 50k annually. Besides, as it can be seen, there is a “?” in the working class category in which we will address later on.

Highest education degree

Code 
income_dataset %>%
  count(education, income) %>% 
  mutate(income = factor(income, levels = c(">50K", "<=50K"))) %>% 
  ggplot(aes(x = fct_reorder(education, n), y = n, fill = income)) +
  geom_col(width = 0.5) +
  coord_flip() +
  scale_y_continuous(labels = comma, limits = c(0, 18000)) +
  labs(title = "Distribution of highest education degree",
       x = "",
       y = "",
       fill = "Income")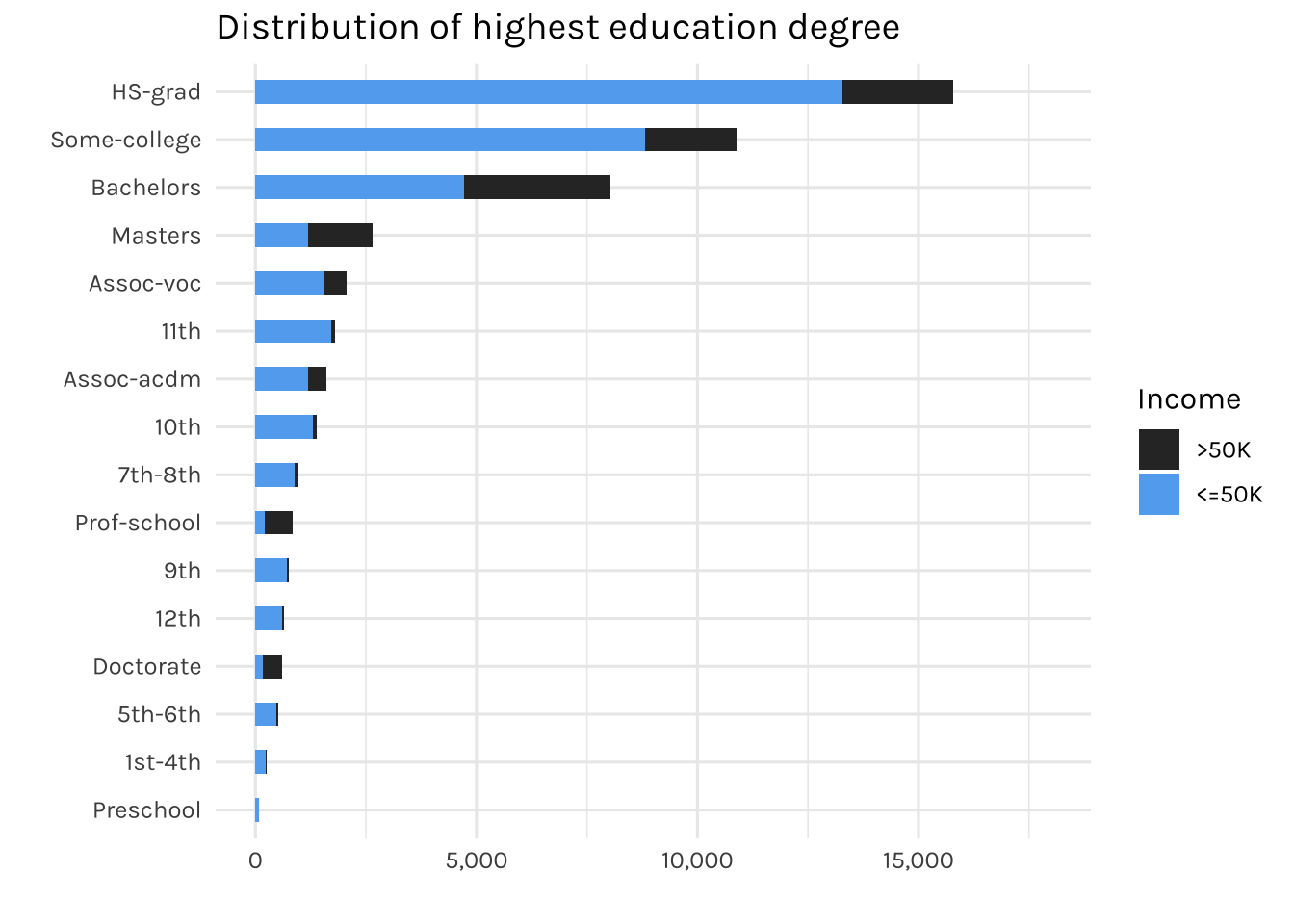

It can be observed that most of the individuals here have a high school degree (HS-grad). Interestingly, there are 83 individuals with only a pre-school education. Let’s see the distribution of income (<=50k or >50k) for individuals who have pre-school as their highest education degree.

Code 
income_dataset %>%
  filter(education == "Preschool") %>% 
  count(income) %>% 
  kable()
income n
<=50K 82
>50K 1

Marital Status

Code 
income_dataset %>% 
  count(`marital-status`, income) %>% 
  mutate(income = factor(income, levels = c(">50K", "<=50K"))) %>% 
  ggplot(aes(x = fct_reorder(`marital-status`, n), y = n, fill = income)) +
  geom_col(width = 0.5) +
  coord_flip() +
  scale_y_continuous(labels = comma, limits = c(0, 25000)) +
  labs(title = "Distribution of marital status",
       x = "",
       y = "",
       fill = "Income")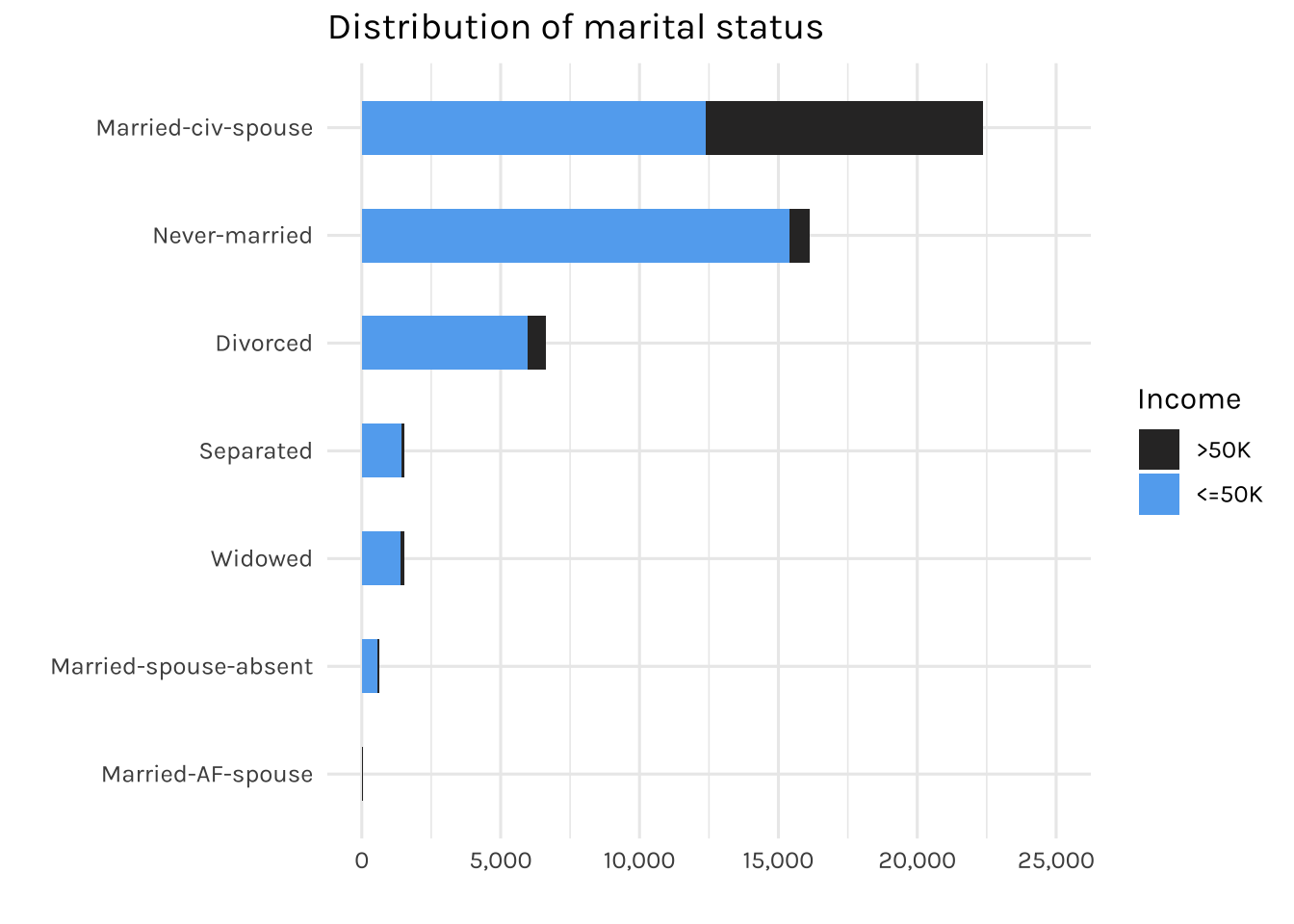

The graph above is showing the distribution of individuals by marital status

Occupation

Code 
income_dataset %>% 
  count(occupation, income) %>% 
  mutate(income = factor(income, levels = c(">50K", "<=50K"))) %>% 
  ggplot(aes(x = fct_reorder(occupation, n), y = n, fill = income)) +
  geom_col(width = 0.5) +
  coord_flip() +
  scale_y_continuous(labels = comma, limits = c(0, 7500)) +
  labs(title = "Distribution of occupation",
       x = "",
       y = "",
       fill = "Income")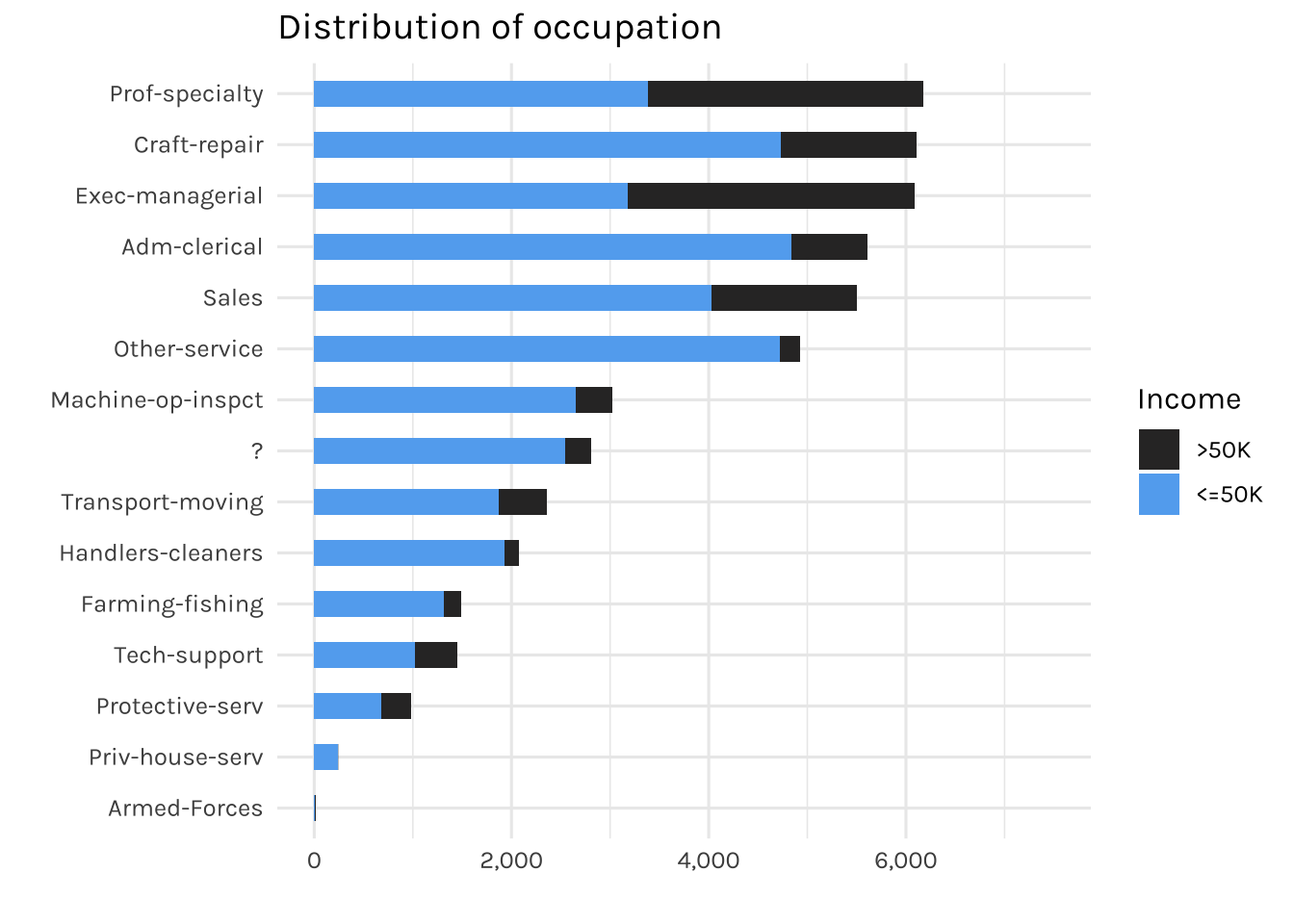

Most individuals are working in expert roles, meanwhile, the fewest (15) are working in the armed forces. Additionally, there is also a “?” present in the occupation feature, which we will deal with later on.

Relationship

Code 
income_dataset %>% 
  count(relationship, income) %>% 
  mutate(income = factor(income, levels = c(">50K", "<=50K"))) %>% 
  ggplot(aes(x = fct_reorder(relationship, n), y = n, fill = income)) +
  geom_col(width = 0.5) +
  coord_flip() +
  scale_y_continuous(labels = comma, limits = c(0, 22000)) +
  labs(title = "Distribution of relationship",
       x = "",
       y = "",
       fill = "Income")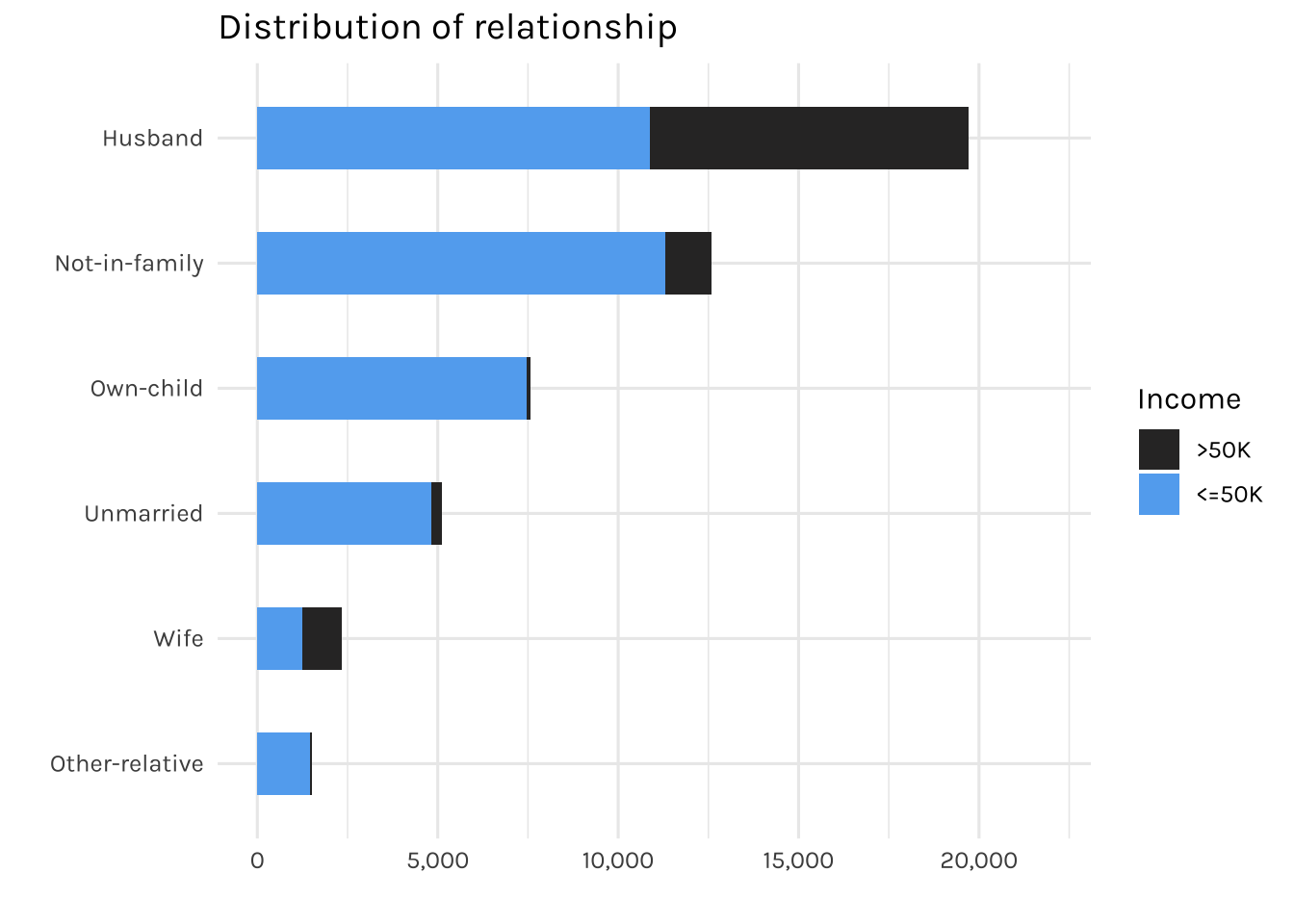

The graph is displaying the relationships recorded in this dataset.

Race

Code 
## Level

desired_level_race <- income_dataset %>% 
  count(race, income) %>% 
  group_by(race) %>% 
  mutate(percentage = round((n / sum(n)) * 100, 2)) %>% 
  filter(income == "<=50K") %>% 
  arrange(percentage) %>% 
  pull(race) %>% 
  unique()

income_dataset %>%
  count(race, income) %>% 
  mutate(race = factor(race, levels = desired_level_race),
         income = factor(income, levels = c(">50K", "<=50K"))) %>% 
  ggplot(aes(x = race, y = n, fill = income)) +
  geom_bar(width = 0.5, position="fill", stat="identity") +
  coord_flip() +
  scale_y_continuous(labels = percent) +
  labs(title = "Percentage of income by race",
       x = "Workclass",
       y = "",
       fill = "Income")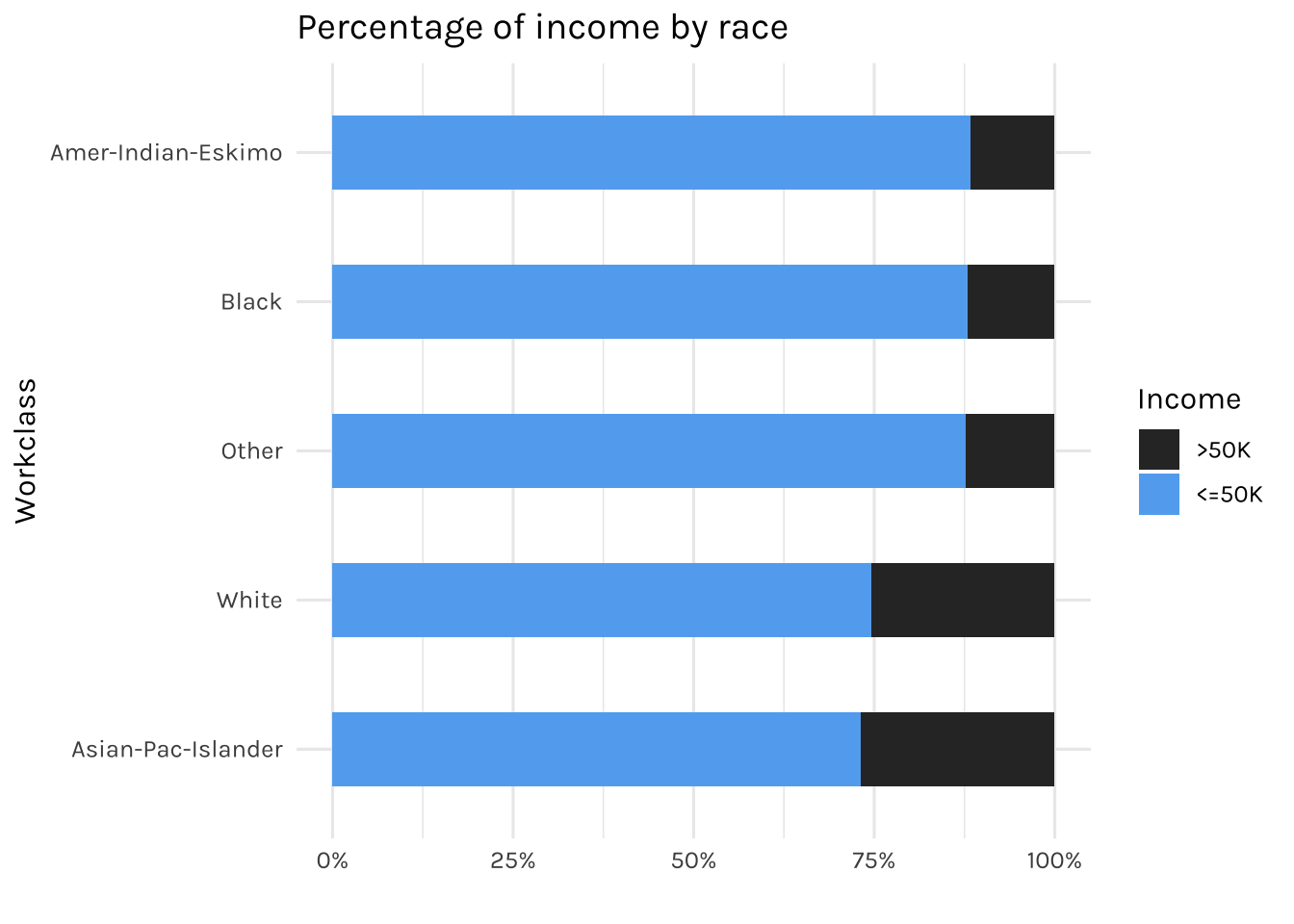

Now the graph above displays the percentage of income (<=50k or >50k) for each race.

Gender

Code 
income_dataset %>%
  count(gender, income) %>% 
  mutate(income = factor(income, levels = c(">50K", "<=50K"))) %>% 
  ggplot(aes(x = fct_reorder(gender, n), y = n, fill = income)) +
  geom_col(width = 0.5) +
  coord_flip() +
  scale_y_continuous(labels = comma, limits = c(0, 35000)) +
  labs(title = "Distribution of gender",
       x = "",
       y = "",
       fill = "Income")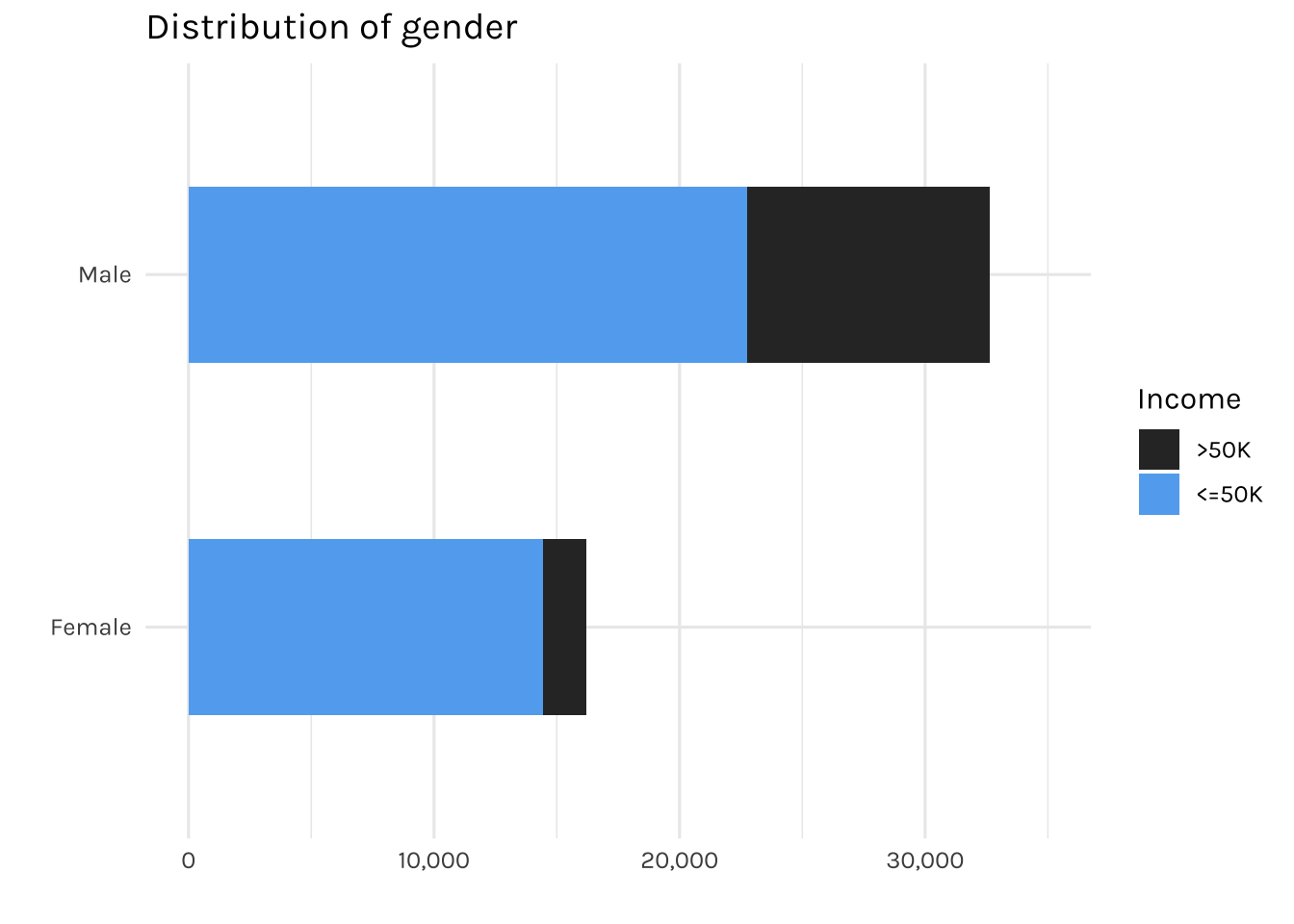

The graph above is showing the total number of individuals by gender. It can be seen that the majority of females are earning less than 50k annually.

Hours per week

Code 
income_dataset %>%
  mutate(`hours-per-week` = case_when(`hours-per-week` < 40 ~ "<40",
                                      `hours-per-week` >= 40 ~ ">=40")) %>% 
  count(`hours-per-week`, income) %>% 
  mutate(income = factor(income, levels = c(">50K", "<=50K"))) %>% 
  ggplot(aes(x = fct_reorder(`hours-per-week`, n), y = n, fill = income)) +
  geom_col(width = 0.5) +
  coord_flip() +
  scale_y_continuous(labels = comma, limits = c(0, 40000)) +
  labs(title = "Distribution of working hours per week",
       x = "",
       y = "",
       fill = "Income")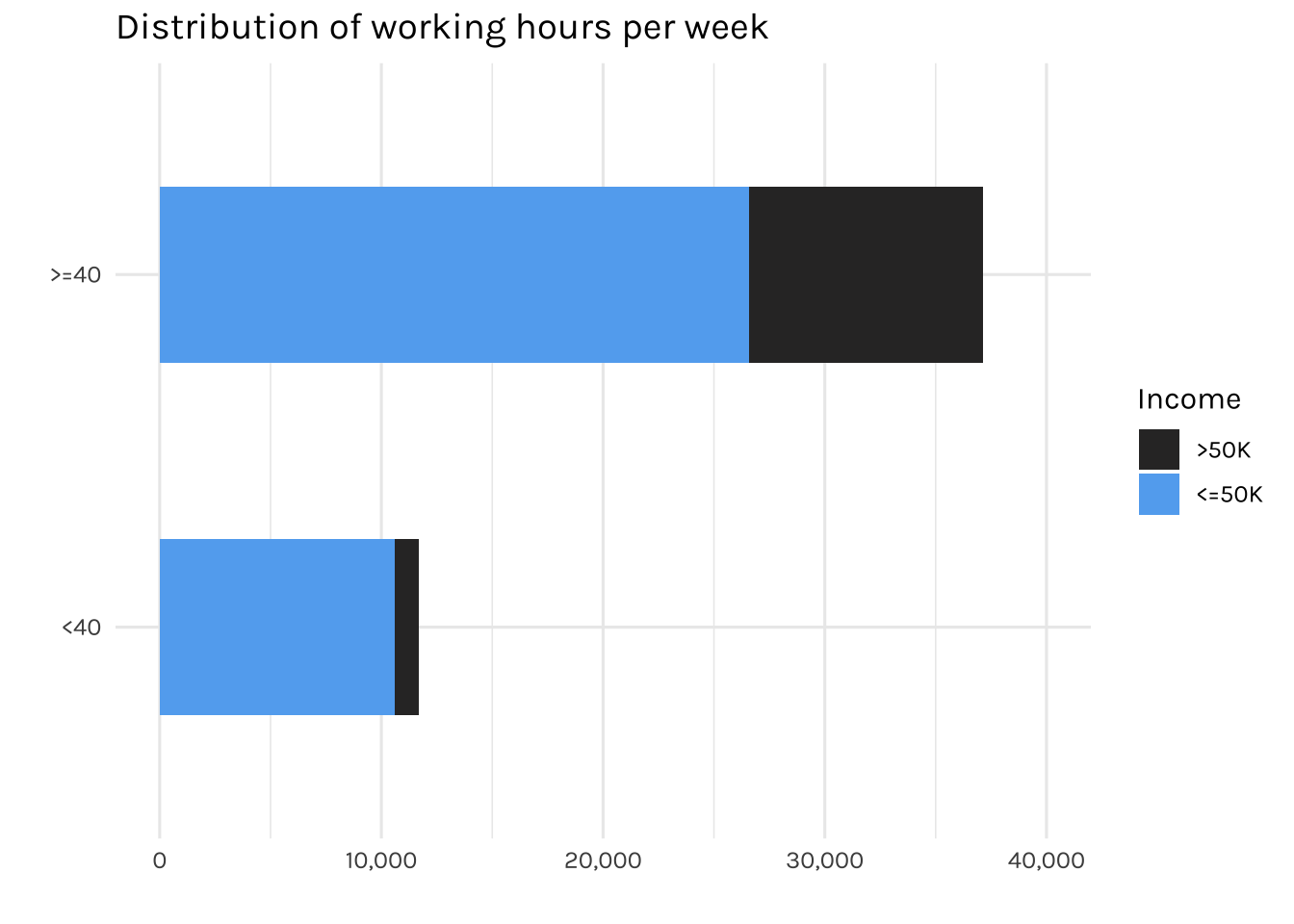

A study by Stanford University indicates that the ideal number of hours for a productive workweek is 35-40 hours. Therefore, for the sake of simplifying the way we analyse the data, we will group working hours as either <40 or >= 40, rather than using the original continuous format.

Native country

Code 
income_dataset %>%
  mutate(`native-country` = fct_lump(`native-country`, prop = 0.05)) %>% 
  count(`native-country`, income) %>% 
  mutate(income = factor(income, levels = c(">50K", "<=50K"))) %>% 
  ggplot(aes(x = fct_reorder(`native-country`, n), y = n, fill = income)) +
  geom_col(width = 0.5) +
  coord_flip() +
  scale_y_continuous(labels = comma, limits = c(0, 50000)) +
  labs(title = "Distribution of countries",
       x = "",
       y = "",
       fill = "Income")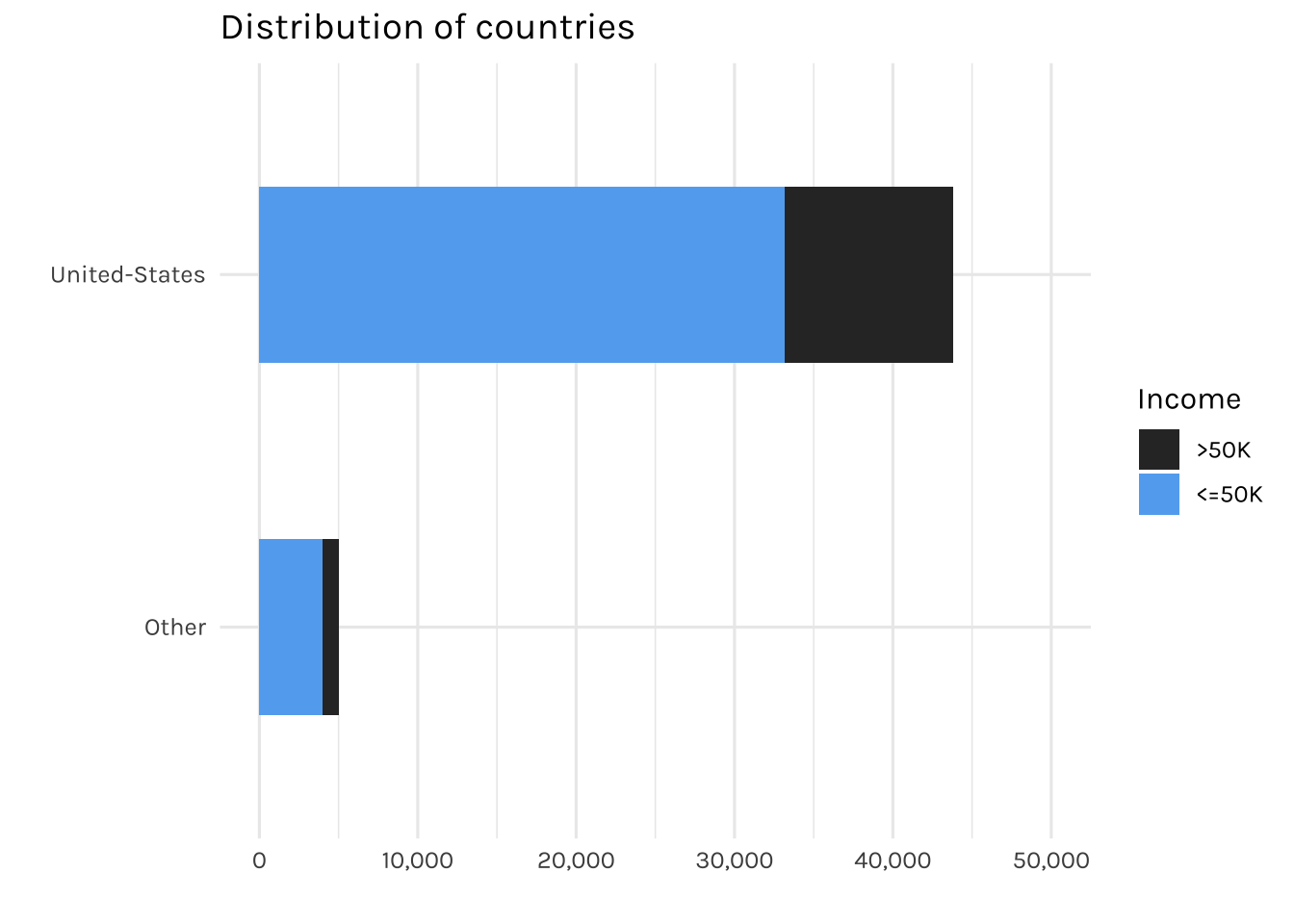

Most of the individuals in this dataset are from the US, with less than 5% are from other countries. Therefore, for countries with less than 5% representation will be grouped into an “Other” category.

Data Preprocessing

Handling “?”

As mentioned earlier, we identified “?” in multiple features of our data set. Hence in this project, we will be treating “?” as missing values to indicate that these values are not available.

Code 
# Calculate percentage of missing values in each column
missing <- income_dataset %>% 
  # Change ? to na
  mutate(across(everything(), ~if_else(. == "?", NA, .))) %>% 
  summarise(across(everything(), ~sum(is.na(.))/n())) %>%
  gather(key = "variable", value = "pct_missing")



# Plot the percentage of missing values
missing %>%
  arrange(desc(pct_missing)) %>%
  ggplot(aes(x = fct_reorder(variable, pct_missing), y = pct_missing)) +
  geom_col() +
  coord_flip() +
  geom_text(mapping=aes(label= percent(pct_missing, accuracy = 0.01), x = variable),
            size= 3, hjust = -0.5) +
  labs(x = "Variable", y = "Percentage of Missing Values", 
       title = "Percentage of Missing Values by Column") +
  scale_y_continuous(labels = percent, expand = c(0,0), limits=c(0,1))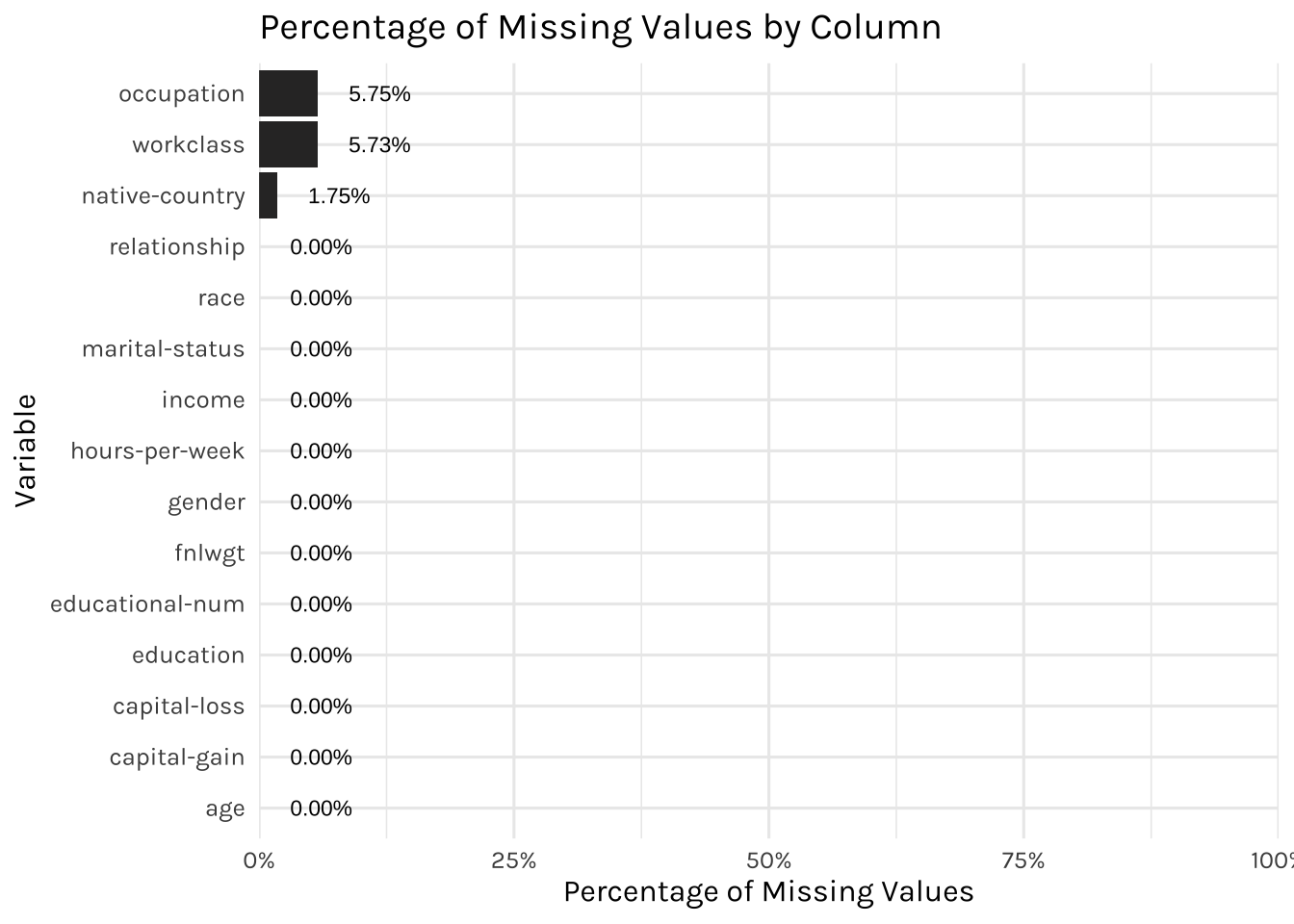

Since the missing values constitute only about 5% in the occupation, workclass & native-country columns, we will remove them from our modelling later on.

Data Modelling

For this project, tidymodels package will be used to split the dataset into training & testing sets, with an 80:20 split ratio

Split dataset

Code 
set.seed(1234)

income_split <- income_dataset |> 
  initial_split(prop = 0.8, strata = income)

income_train <- training(income_split)
income_test <- testing(income_split)

Cross validation

Cross validation: A technique often used to estimate the generalization error of the models, which would be the error that the models make on new, unseen data.

In our project, we will be applying k-fold cross validation; where the data will be split into k folds, and the model is trained and tested k times. To save time and resources, we are using a 5-fold cross-validation.

Code 
income_folds <- vfold_cv(income_train, v = 5, strata = income)

Define recipe (s)

  1. Removing missing values
  2. Removing `educational-num` column, similar to education column, just in code format
  3. Grouping hours per week (<40 or >=40)
  4. Grouping together fewer countries (Countries with less than 5% representation will be grouped into an “Other” category
  5. Transforming categorical variables into a numerical format to be used in our model
  6. Removing columns with zero variance. Columns with zero variance have the same value for every row in the data, and therefore do not provide any useful information for the model
  7. Normalizing columns: Can be useful in a number of situations, such as when the features of the training dataset have different scales or units

We will be applying three concepts:

  • Baseline (no sampling technique applied),

  • Downsampling

  • Upsampling

Baseline

No class imbalance technique is applied to handle class imbalance (income)

Code 
income_baseline_rec <- income_train %>%
  recipe(income ~ .) %>%
  step_filter(workclass != "?", occupation != "?", `native-country` != "?") %>% 
  step_rm(`educational-num`) %>% 
  step_mutate(`hours-per-week` = case_when(`hours-per-week` < 40 ~ "<40",
                                      `hours-per-week` >= 40 ~ ">=40")) %>% 
  step_string2factor(`hours-per-week`) %>% 
  step_other(`native-country`, threshold = 0.05, other = "Other") %>% 
  step_dummy(all_nominal(), -all_outcomes()) %>% 
  step_zv(all_numeric_predictors()) %>%
  step_normalize(all_numeric_predictors()) 

income_baseline_rec

Downsample

We will be applying downsampling technique. It is a technique used to handle class imbalance in a dataset. In the context of this Adult income dataset, downsampling could be applied to reduce the number of <=50K to a level that is more balanced with the number of >50K.

Code 
income_downsample_rec <- income_baseline_rec %>% 
  step_downsample(income)

income_downsample_rec

Upsample

We will be applying upsampling technique. This is a technique used to duplicate existing instances in the >50K class, bringing the number of >50K to a level that is more balanced with the number of <=50K.

Code 
income_upsample_rec <- income_baseline_rec %>% 
  step_upsample(income)

income_upsample_rec

Define models

Logistic Regression

Predictive modeling is developed using Logistic Regression:

Code 
## Logistic
glm_set <- logistic_reg() %>%
  set_engine("glm")

glm_set
Logistic Regression Model Specification (classification)

Computational engine: glm

SVM

We will also develop Linear Support Vector Machine:

Code 
svm_set <-
  svm_linear() %>%
  set_mode("classification") %>%
  set_engine("LiblineaR")

svm_set
Linear Support Vector Machine Model Specification (classification)

Computational engine: LiblineaR

Define models in workflow

We will now be employing a tidymodels workflow to fit logistic regression & SVM models which allows to easily compare between the two models and also preprocess the data using the recipes defined earlier.

Code 
## Set workflow

income_models <-
  workflow_set(
    preproc = list(
      baseline = income_baseline_rec,
      downsample = income_downsample_rec,
      upsample = income_upsample_rec
    ),
    models = list(glm = glm_set,
                  svm = svm_set),
    cross = TRUE
  )


set.seed(1234)
doParallel::registerDoParallel()

## Fit models

income_rs <-
  income_models %>%
  workflow_map(
    resamples = income_folds,
    metrics = metric_set(accuracy, sensitivity, specificity, precision)
  )

Model evaluation

Comparing the performance of Logistic Regression and Linear SVM in the table below:

In our baseline models, we are performing very well in terms of the sensitivity values but not specificity. This is due to the slight imbalance in our income (target variable), hence it affects the models’ ability to classify the minorities very well

This is where undersampling & oversampling help to handle the class imbalance. While they may reduce the sensitivity values slightly, but they significantly improve the specificity values, which also are very important for our analysis. Although both models performed fairly well, we will be going for SVM (downsample) as it has slightly higher specificity and precision.

Code 
collect_metrics(income_rs) %>% 
  ## select only necessary columns
  select(wflow_id,model, .metric, mean) %>% 
  ## round off
  mutate(mean = round(mean,4)) %>% 
  mutate(wflow_id = case_when(str_detect(wflow_id, "baseline") ~ "Baseline",
                              str_detect(wflow_id, "downsample") ~ "Downsample",
                              str_detect(wflow_id, "upsample") ~ "Upsample")) %>% 
  pivot_wider(names_from = model,
              values_from = mean) %>% 
  rename(`Logistic Regression` = logistic_reg,
         `SVM Linear` = svm_linear) %>% 
  reactable(filterable = T,
            columns = list(
              `Logistic Regression` = colDef(
                cell = data_bars(., 
                       fill_opacity = 0.8, 
                       text_position = "above",
                       number_fmt = scales::percent_format(accuracy = 0.01))),
              
               `SVM Linear` = colDef(
                cell = data_bars(., 
                       fill_opacity = 0.8, 
                       text_position = "above",
                       number_fmt = scales::percent_format(accuracy = 0.01)))
  ))

Fitting final model

Having obtained satisfying performance on the training set, we would then apply the SVM (undersample) model to the test data.

Code 
## getting the best model
best_workflow <- collect_metrics(income_rs) %>% 
                      filter(.metric == "specificity") %>% 
                      slice_max(mean) %>% 
                      pull(wflow_id)


final_wf <- extract_workflow(income_rs, best_workflow)


final_fit <- last_fit(
    final_wf,
    income_split,
    metrics = metric_set(accuracy, sensitivity, specificity, precision)
  )

collect_metrics(final_fit) %>% 
  select(.metric, .estimate) %>% 
  rename(Metric = .metric,
         Value = .estimate) %>% 
  reactable(filterable = T,
            columns = list(
              Value= colDef(
                cell = data_bars(., 
                       fill_opacity = 0.8, 
                       text_position = "above",
                       number_fmt = scales::percent_format(accuracy = 0.01)))
  ))

Meanwhile, this is the confusion matrix:

Code 
collect_predictions(final_fit) %>%
  conf_mat(income, .pred_class) %>% 
  pluck(1) %>%
  as_tibble() %>%
  ggplot(aes(Prediction, Truth, fill = n)) +
  geom_tile(show.legend = FALSE, alpha = 0.2) +
  scale_fill_gradient2(low = "#CCCCCC",
                       mid = "#FFFFCC",
                       high = "#aaaaaa") +
  geom_text(aes(label = n), alpha = 1, size = 4) +
  theme(panel.grid = element_blank())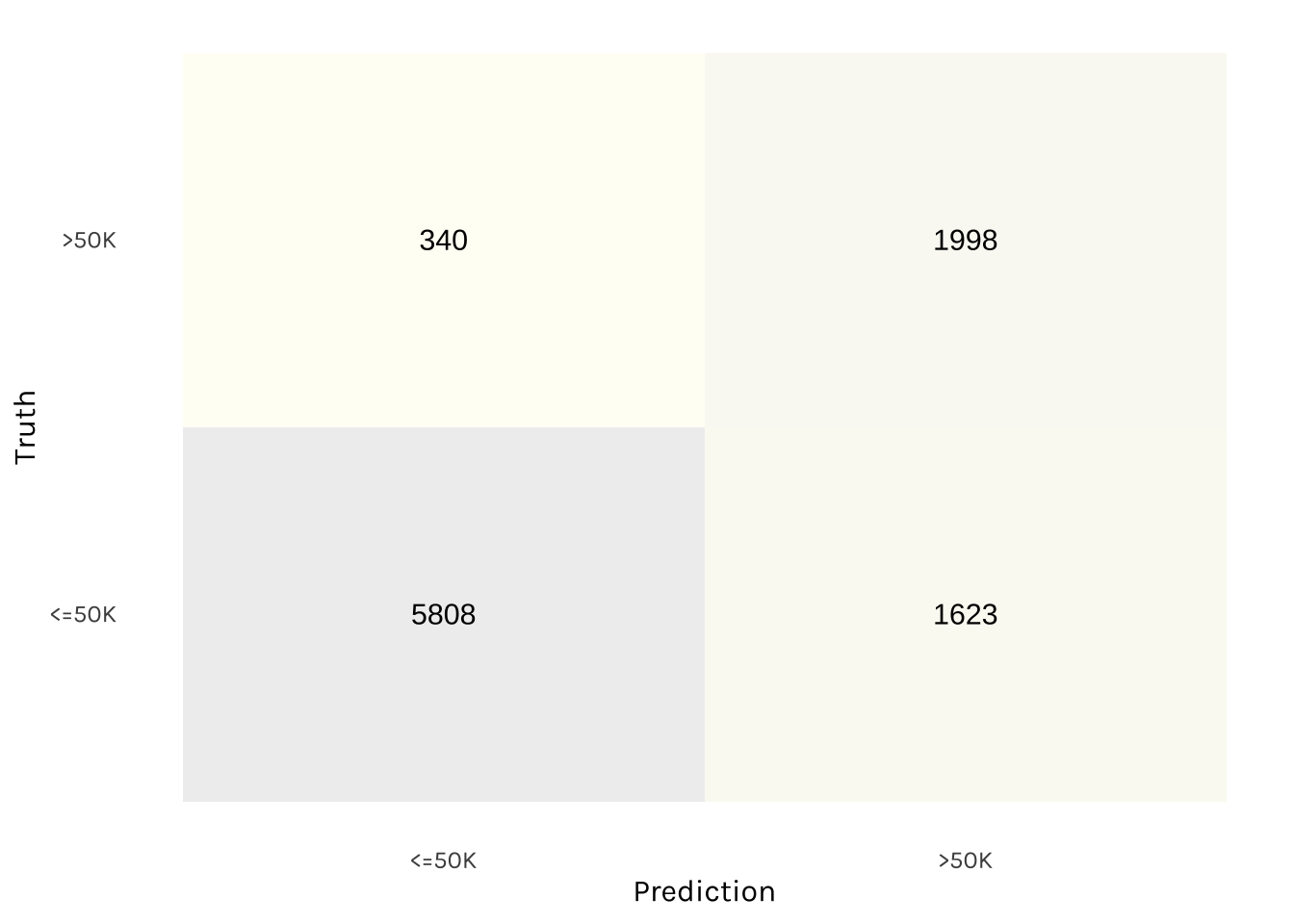

Conclusion

Based on the test data, the SVM (undersample) model performed fairly well. These results demonstrate that the model’s ability to classify a high percentage of both “<=50K” and “>50K” on the test data, making it a reliable and accurate choice for our application.